$$sqrt{2}$$ is superior to Bessel's correction

… for the estimation of the population standard deviation. That is, if you substitute $$n – 1$$ with $$n – \sqrt{2}$$, you get a much less biased estimate of the population SD. I just stumbled upon this when I desperately (!) looked to frequentist methods because of convergence problems with my bayesian model. The details can be seen in my post on Cross Validated about this curious finding as well as some excellent answers/elaborations.

I’m re-posting the simulation results here, just because they’re pretty and I want some content on this blog.

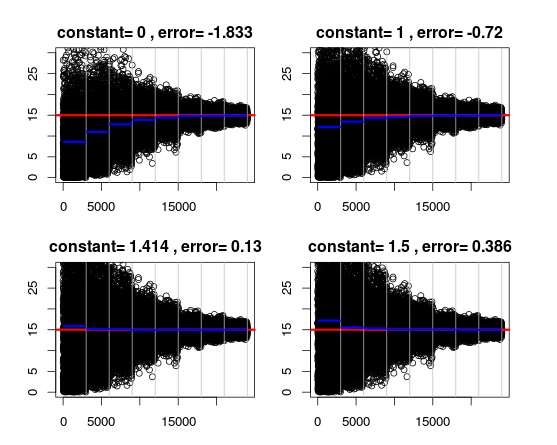
TL: no correction. TR: Bessel’s correction. BL: $$\sqrt{2}$$ correction (superior). BR: 1.5. Red: real population sd. Blue: estimated sd (corrected). Gray lines indicate different sample size with 3000 simulations per sample size. Click on the image to view the script.

Naturally, $$\sqrt{2}$$ doesn’t outperform the analytically correct solution but it is a surprisingly good approximation. For larger sample sizes (n > 10), $$n – 1.5$$ becomes superior. In any case, it’s a nice reminder that Bessel’s correction does NOT magically make the sample SD into a population SD as is currently taught in many statistics classes.

I’m considering adding this fun-fact to the Wikipedia page on unbiased estimation of the standard deviation, where you can read more about the issue of bias in frequentist estimation.