TL;DR: I just published “Reaction Time Distributions – An Interactive Overview“.
There is a big literature on the analysis of Reaction Time data. Everybody can see that reaction times are not normally distributed but there is little consensus about how they are distributed. This has resulted in many advanced mathematical arguments why one or the other distribution is better. Others propose obscure rules-of-thumb ways of deleting or transforming data so that it looks normally distributed.
Meanwhile, the average researcher is left bewildered, often resorting to some variant of the normal distribution which they know and love from other kinds of data. This is worse than any of the alternatives as would be obvious to anyone who did a proper assessment of their model fit, e.g., using a QQ-plot, a Shapiro-Wilk test, or a posterior predictive check.
I think that we need a guide so accessible that it lowers the bar just enough that people jump aboard trying different RT distributions. Long story short, I ended up writing an overview and presented it in a twitter thread:
The easy part: making it.
I myself have been bewildered about analyzing reaction times. It was only when I discovered the flexible distributional regression in brms, that I took a few alternative distributions for a spin on a dataset I was working on. The superior fit immediately did away with all the problems I had been hacking myself out of.
- The model fits faster and more reliably.
- You need not transform the data and you need less outlier removal.
- The model predictions actually look like the data you are modeling.
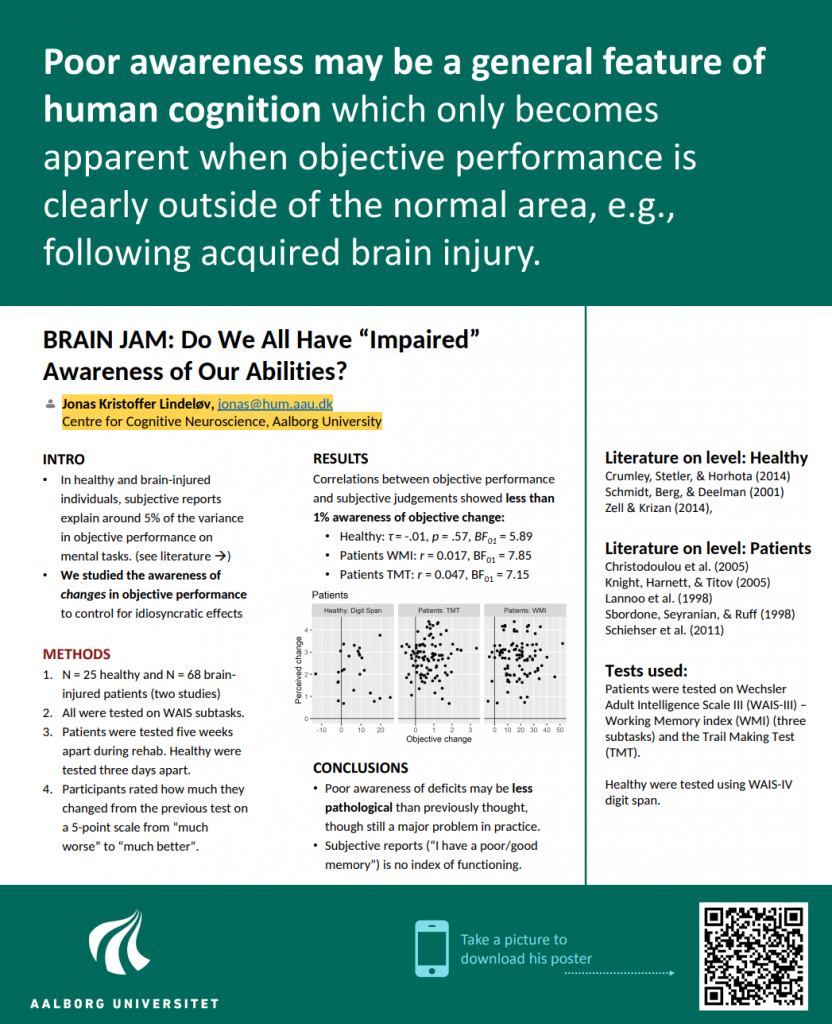
Naturally, the fit was superior to a Gaussian. A leave-one-out Cross-Validation found that the log-predictive error was halved! Here is a figure from an upcoming paper:
A few weeks later, I spent an evening checking out `shiny` to make interactive plots. Two evenings later, I had written most of the guide/overview. It was so easy. ` shiny ` made interactivity a breeze and ` brms` (and ` rtdists`) had PDFs for most of the distributions. It was just a matter of connecting the two. Another evening for the cheat sheet, and I was ready to put it online (this was the hard part; see below).
Warning: it’s also an opinion.
As the interactivity allowed me to get intuitions about the distributions myself, I grew quite opinionated because some distributions were really hard to get intuitions about.

Take for example the very popular ex-gaussian. The added exponential decay completely changes the mean and the standard deviation so that, e.g., μ = 0.4 secs and σ = 0.2 secs does not refer to anything identifiable in the distribution. Furthermore, the exponential parameter (λ) is very hard to understand, and in most analyses, I’ve seen it’s discounted. This means that they essentially say “all long RTs are not really RTs but something else” which I find odd. μ systematically underestimates RTs.
We want one parameter to capture most of what RTs are about, and I ended up going with the term “Difficulty” for that parameter cf. Wagenmakers & Brown (2007). I explain why in the overview, but briefly, it allows you to do univariate regression everybody does anyway. I haven’t seen this argument put forward elsewhere so I guess it counts as an opinion.
My favorites generic distributions are the shifted log-normal and the Decision Diffusion model as is also clear from the cheat sheet. Of course, people should choose on a case-by-case basis.
The hard part: hosting it.
The hard part was getting this to run on the web, which required around 6 evenings and a lot of debugging. shinyapps.io is very convenient for RStudio users, but the server shuts down after a document has been in use for 25 hours in a month. I choose to set up a shiny server using Google Cloud because they offered a year’s worth of free computing and pretty low charges after that. I followed this guide.
However, I encountered heaps of issues which I’ve explained in the document’s GitHub repo. The current solution is good enough, but some issues remain.