Let’s rename “fixed” to “Population-level” and “Random” to “Varying”

1. March 2018 12. November 2020

I was reading this interesting preprint on ordinal regression by Paul Bürkner and Matt Vuorre. Now see this footnote about their vocabulary:

Hallelujah and Eureka!! I think that these terms may help solve (some of) the long-standing confusion about the difference between “fixed” and “random” effects.

TL;DR: To shrink or not to shrink – that is the question

The mathematical distinction is that Varying (“random”) parameters have an associated variance while Population-level (“fixed”) parameters do not. Population-level effects model a single mean in the population. Varying effects model a mean and a variance term in the population, i.e., two rather than one parameters. The major practical implication is that Varying parameters have shrinkage in a regression towards the mean-like way whereas the Population-level parameters do not.

The figure below shows this shrinkage in action for the following three models:

fit_varying = lme4::lmer(WMI ~ session + (1|id), D)  # Varying subject-intercept (red lines)
fit_population = lm(WMI ~ session + id, D)  # Population-level subject-intercept (blue lines)
fit_mean = lm(WMI ~ session, D)  # No subject-intercept (black lines)

The figure shows five illustrative participants (panels), each tested four times. A model with varying subject-intercept (red lines) shrinks subjects closer to the group mean (black line) than the model with the population-level subject-intercept (blue lines). The green lines are actual scores. Furthermore, the shrinkage is stronger the further away the data is from the overall mean. See the accompanying R notebook for all details and all participants.

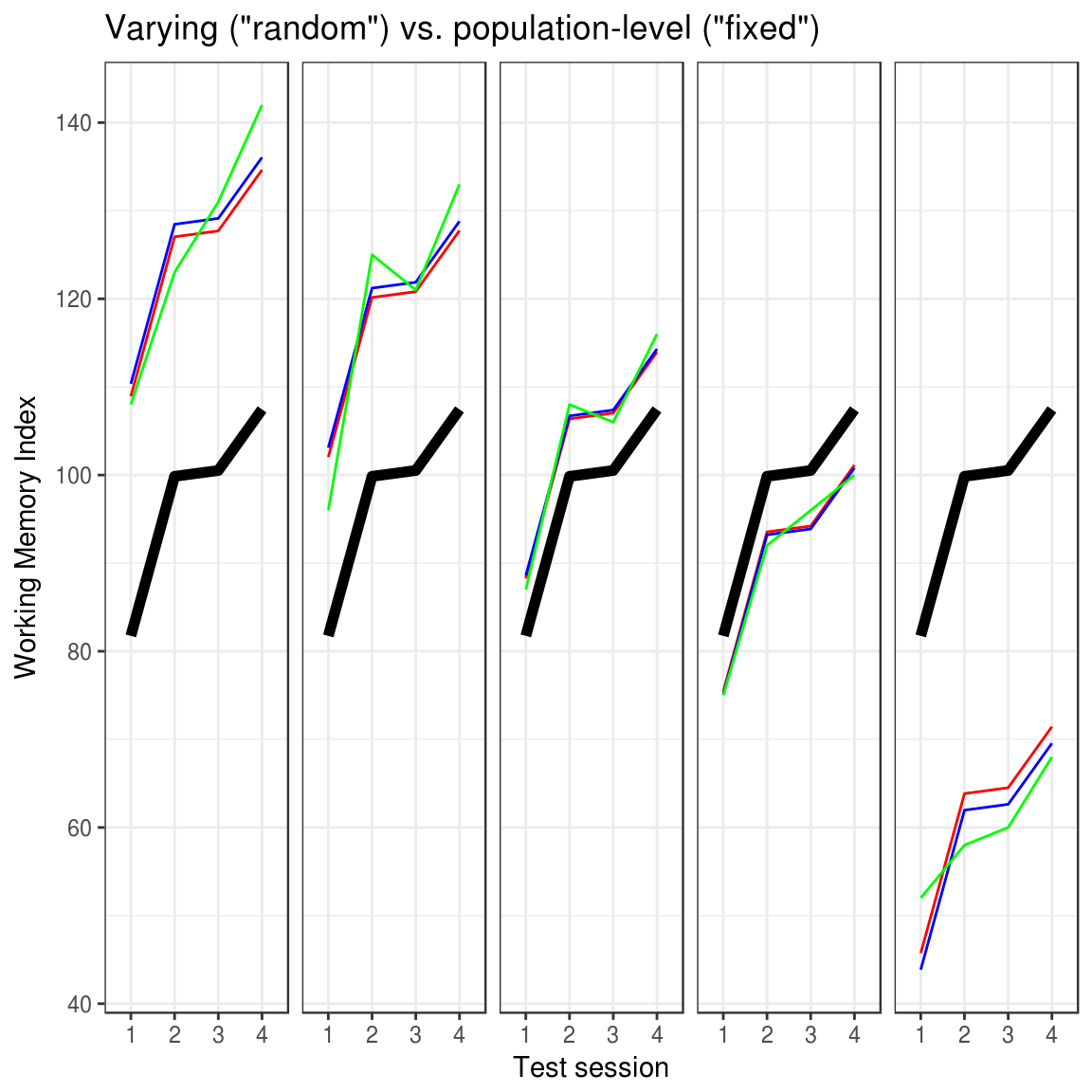
So shrinkage is the only practical difference. This is true for both frequentist and Bayesian inference. Understanding when to model real-world phenomena using shrinkage, however, is not self-evident. So let me try to unpack why I think that the terms “Population-Level” and “Varying” convey this understanding pretty well.

Population-level parameters

General definition:

Values of Population-level parameters are modeled as identical for all units.

Example:

Everybody in the population of individuals who could ever be treated with X would get an underlying improvement of exactly 4.2 points more than had they been in the control group. Mark my words: Every. Single. Individual! The fact that observed changes deviate from this true underlying effect is due to other sources of noise not accounted for by the model.

The example above could be a 2×2 RM-ANOVA model of RCT data (outcome ~ treatment * time + (1|id)) with treatment-specific improvement (the treatment:time interaction) as the population-level parameter of interest. Populations could be all people in the history of the universe, all stocks in the history of the German stock market, etc. Again, the estimated parameters are modeled as if they were exactly the same for everyone. The only thing separating you from seeing that all-present value is a single residual term of the model, reflecting unaccounted-for noise. The residual is an error term so it is not the model itself. As seen from the model, everybody is identical and the residual is simply an error term (which is not part of the model) indicating how far this view of the world deviates from observations.

I think that modeling anything as a Population-level parameter is an incredibly bold generalization of the sort that we hope to discover using the scientific method: the simplest model with the greatest predictive accuracy.

Now, it’s easy to see why this would be called “fixed” when you have a good understanding of what it is, but as a newcomer, the term “fixed” may lead you astray thinking that either (1) it is not estimated, (2) that it is fixed to something, or that its semantically self-contradictory to call a variable fixed! Andrew Gellman calls them non-varying parameters, and I think this term suffers a bit from the same possible confusions. Population-level goes a long way here. The only ambiguity left is whether parameters that apply to the population also apply to individuals, but I can’t think of a better term. “Universal”, “Global”, or “Omnipresent” are close competitors but they seem to generalize beyond a specific population so let’s stick with Population-level.

Varying parameters

General definition:

Values of Varying parameters are modeled as drawn from a distribution.

Example for (1|id) :

Patient-specific baseline scores vary with SD = 14.7.

Example for (0 + treatment:time | id) :

The patient-specific responses to the treatment effect vary with SD = 3.2 points.

This requires a bit of background explaining so bear with me: Most statistics assume that the residuals are independent. Independence is a fancy way of saying that if you know any one residual point, you would not be able to guess above chance about any other residuals. Thus, the independence assumption is violated if you have multiple measurements from the same unit, e.g., multiple outcomes from each participant since knowing one residual from an extraordinary well-performing participant would lead you to predict above-chance that other residuals from that participants would also be positive.

You could attempt to solve this by modeling a Population-level intercept for each participant (outcome ~ treatment * time + id), effectively subtracting that source of dependence in the model’s overall residual. However, which of these participant-specific means would you apply to an out-of-sample participant? Answer: none of them; you are stuck (or fixed?). Varying parameters to the rescue! Dropping the ambition to say that all units (people) exhibit the same effect, you could estimate the recipe on how to generate those intercepts for each participant which helped you get rid of the dependence of the residuals (or more precisely: model it as a covariance matrix). This is a generative model in the form of the parameter(s) of a distribution and in GLM this would be the standard deviation of a normal distribution with mean zero.

One way to represent this clustering of variation to units is a hierarchical model where outcomes are sampled from individuals which are themselves sampled from the nested Population-level parameter structure:

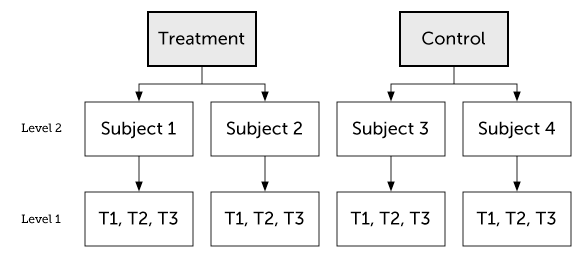
Two-level multilevel model in r. By Kristoffer Magnusson — Figure by Kristoffer Magnusson. Click to see the source which includes R code to fit this model and many more.

For this reason, I think that we could also call Varying parameters sampled parameters. This is true whether those sampled parameters are intercepts, slopes, or interaction terms. Crossed Varying effects are just parameters sampled from the joint distribution of two non-nested populations (e.g., subject and questionnaire item). Simple as that!

Again, it’s easy to see why one would call this a “random” effect. However, as with “fixed effects,” it is just easy to confuse this for (1) the random-residual term in the whole model, or (2) the totally unrelated difference between frequentist and Bayesian inference as to whether data or parameters are fixed or random. Varying seems to capture the what it’s all about – that units can vary in a way that we can model. With variation comes regression towards the mean so it follows naturally.

Two derived properties of Varying

Firstly, it models regression towards the mean for the varying parameters: Extreme units are shrunk towards the mean of the varying parameter since those units are unlikely to reflect a true underlying value. For example, if you observe an exceptionally large treatment effect for a particular participant, he or she is likely to have experienced a lesser underlying improvement, but unaccounted-for factors exaggerated this by chance. Similarly, when you observe exceptionally small observed treatment effects, it is likely to reflect a larger underlying effect masked by chance noise.

Secondly, it requires enough levels (“samples”) of the Varying factor to estimate its variance. You just can’t make a very relevant estimate of variance using two or three levels (e.g. ethnicity). Similarly, sex would definitely make no sense as Varying since there is basically just two levels. Participant number, institution, or vendor would be good for analyses where there are many different of those. For frequentist models like lme4::lmer, a rule of thumb is more than 5-6 levels. For Bayesian models, you could have even one level (because Bayes rocks!) but the influence of the prior and the width of the posterior would be (unforgivably?) big.

Some potential misunderstandings

I hope that I conveyed the impression that the distinction between Population-level and Varying modeling is actually quite simple. However, the Fixed/Random confusion has caused people to exaggerate their difference for illustrative purposes, giving the impression that they do have distinct “magical properties”. I think they are more similar:

Both random and fixed can de-correlate residuals: It is sometimes said that you model effects as “fixed” to model effects of theoretical interest and other effects as “random” to account for correlated residuals, thus respecting the independence assumption (e.g., repeated measures). However, both “fixed” and “random” effects de-correlate residuals with respect to that effect. No magic!

Both random and fixed can account for nuisance effects: It is often said that random effects are for nuisance effects and fixed effects model effects of theoretical importance. However, as with the point above about de-correlating residuals, they can both do this. Say you want to model some time-effect (e.g., due to practice or fatigue) of repeated testing to get rid of this potential systematic disturbance if your theory-heavy parameters. You could model time as a fixed effect and just ignore its estimate or you could model it as random. The decision should not be theory vs. nuisance but rather whether the effect of time is modeled as identical for everyone or as Varying between units. No magic!

Both Varying and Population-level are model population-wide parameters. The word “population-level” effect may sound like it is the only parameter that says something about the population or that it is easier to generalize. In fact, I highlighted above that for “sampled” parameters, it was easier to see how Varying effects would generalize. Is this self-contradictory? No. Population-level effects are the postulate that there is a single mean in the population. Varying effects are the postulate that there is a mean and a variance term in the population.

Helpful sources

A few sources that helped me arrive at this understanding was:

Here are some nice visualizations of “fixed” vs. “random” effects in the context of meta-analyses. The distinction is the same. Instead of “study”, just think “participant”, “country”, or whatever.
Writing mixed models in BUGS helped me to de-mysticise most of linear models, including fixed/random and what interactions are. I started in JAGS. Here’s a nice example.
This answer on Cross-Validated which made me realize that shrinkage is the only practical difference between modeling parameters as “fixed” or “random.”
The explanation in the FAQ to R mailing list on GLMM, primarily written by the developers of the lme4 package.
Brauer & Curtin (2017) with plain-language recommendations for mixed models.
Hodges & Clayton (2011) makes a distinction between “old-style” random effects (draws from a population), which I have mentioned here, and “new-style” random effects where the variance term is used more for mathematical convenience, e.g. when there is no population, the observed units exhaust the population, or when no new draws are possible. It is my impression that “new-style” is seldom used in psychology and human clinical trials.

TO DO

IMPORTANT: Rename terms? Varying is just two population-level parameters instead of one. How about: “
Mention that population-level has superior fit to data.
Fix plot annotations
Varying as uncertainty around fixed and residual as errors from model!
Use intro model in the quotes below
Fixed vs. random well-known in MA
Add legend to figure

New tutorial on computing Bayes factors in R

11. February 2018 8. April 2019

I just published a practical guide on computing Bayes factors using various packages in R. Head over to RPubs and check out How to compute Bayes factors using lm, lmer, BayesFactor, brms, and JAGS/stan/pymc3.

My first goal is to present solutions to things that I found difficult in the respective packages and which are relatively undocumented. A second goal was to show a side-by-side comparison on whether the packages converge on the same Bayes factor estimates.

I hope to keep the document updated. In particular, I’m keeping an eye on the development of, BASand I need to learn how to specify a full JZS prior in brms.

Personally, this is a lot of firsts for me and took way too much time: my first R notebook (including Markdown), first tutorial in many years, and first use of brms and BAS.

Software for graphical models

23. November 2017 31. July 2022

I’m currently writing a paper on a new Bayesian method for scoring Complex Span tasks. I needed some software to represent it using plate notation of a directed acyclic graph (DAG). Many people have pointed to the Tikz/pgf drawing library for latex, but I did not want to install latex for this simple task. Here I briefly review yEd, Daft, and Libreoffice Draw.

yEd

I ended up using yEd and produced this graph which contains plates, estimated nodes, deterministic nodes (double-lined), observed nodes (shaded), and categorical nodes (rectangles).yEd is purely graphical editing which is fast to work with and great for tweaking small details. A very handy yEd feature is its intelligent snapping to alignments and equal distances when positioning objects. Actually, I don’t understand why yEd almost never makes it to the “top 10 diagram/flowchart programs” lists.

A few things I learned: To make subscripts, you have to use HTML code. For example, the $R_{trial_{i,j}}$ node is

<html>R<sub>trial i,j</sub></html>

However, it is not possible to do double-subscripts. Also, the double-edges node is made completely manually by placing an empty ellipse above another. I did not manage to align the $WMC_i$ label a bit lower in the node. A final limitation is that arrowhead sizes cannot be changed. You can, however, zoom. Therefore, your very first decision has to be the arrowhead size. Zoom so that it is appropriate and make your graphical model. I didn’t think about this so the arrows are too large for me in the graph above.

I’m pretty pleased with the result. For the final paper I may try and redo this in Libreoffice Draw to see if I can fix the final details.

Libreoffice Draw

In retrospect, I think that Draw could have done better than yEd. First, you can scale arrowheads to your liking! Furthermore, you can write math in LibreOffice Math, so double-subscripting is no problem. However, you have to group a math object with an ellipse rather than entering it as “content”, which is a bit convoluted. Speaking of math, LibreOffice Math was great for entering the model specifications for the graphical model:

One small annoyance is that you have to choose between left-aligning everything including the denominators in fractions (which of course should be centered), or center-align everything. I would have liked a center-aligned denominator while left-aligning everything lines.

The above was created using the following code. The matrix was used to align the terms.

matrix{
    alignr %mu     # "~" # "Gamma"(4, 1) ##
    alignr %sigma  # "~" # "Gamma"(3, 2) ##
    alignr WMC_i   # "~" # "Gamma"(%mu, %sigma) " or Poisson"( %mu ) ##
    alignr R_WMC   # "~" # "Beta"(1, 1) ##     alignr R_other # "~" # "Beta"(1, 1) ##
    alignr R_{trial_{i,j}} # "=" # left lbrace matrix {
         R_WMC # if N_{i,j} <= WMC_i ##
         (R_WMC WMC_i + R_other(N_{i,j} - WMC_i))/N_{i,j} # if N_{i,j} > WMC_i } right none ##
    alignr N_recalled # "~" # "Binomial"(R_{trial_{i,j}}, N_{i,j})
}

I have to say that there’s something to the lacking snap-to-alignment and the general interface in Draw that makes it feel less nice than yEd, even though it is probably more versatile for the present purpose. I may update this blog post with a Draw model when I get around doing it.

Daft

Daft is a python module for rendering graphical models. The syntax is quite nice, but I quickly learned that you have to choose between shaded or double-edged nodes as indicators of observed variables. You cannot have both. You can draw an empty smaller node on top to make it double-edged, but using the $scale$ argument makes it non-aligned with the outer line. I raised this as a GitHub issue [UPDATE: Check the GitHub issue – it has been fixed now! I haven’t updated this post]~~, but Daft has not been maintained for years, so I don’t expect this to be fixed~~. Also, you have to install an old fork to draw rectangular nodes. This is as far as I got:

Here’s the code to do it, very much inspired (/ripped off) by this example.

# Set it up 
import daft pgm = daft.PGM([5, 5], origin=[-2.5, -2.5]) 

# Nodes for R_trial 
pgm.add_node(daft.Node('R_WMC', '$R_{WMC}', -1.5, 2, aspect=1.5)) 
pgm.add_node(daft.Node('R_other', '$R_{other}', -0.5, 2, aspect=1.5)) 
pgm.add_node(daft.Node('x', '', -1, 1, scale=0.85, aspect=1.5))  

# Inner ellipse 
pgm.add_node(daft.Node('R_trial', '$R_{trial_{i,j}}', -1, 1, aspect=1.5)) 
pgm.add_edge('R_WMC', 'R_trial') 
pgm.add_edge('R_other', 'R_trial') 

# Nodes for WMC 
pgm.add_node(daft.Node('mu', '$\mu', 0.5, 2)) 
pgm.add_node(daft.Node('sigma', '$\sigma', 1.5, 2)) 
pgm.add_node(daft.Node('WMC', '$WMC_i', 1, 1, aspect=1.5)) 
pgm.add_edge('mu', 'WMC') pgm.add_edge('sigma', 'WMC') 

# Observed N 
pgm.add_node(daft.Node('N', '$N_{i,j}', 0, 0.5, observed=True))
pgm.add_edge('N', 'R_trial') # Subject plate
pgm.add_plate(daft.Plate([-2, 0, 4, 1.5], label='subject $i)) 

# Render it 
pgm.render() 
pgm.figure.savefig("daft graphical model.png", dpi=150)

Some notes

Rob Zinkov posted an interesting argument on how generative stories can be used instead of plate notation.
For those used to R, the ggdag package seems like a really convenient way to draw quick DAGs from formulas.

Five divided by forty-nine

19. November 2017 21. November 2017

At a family dinner, my brother told me that he had stumbled upon a curious number. Divide five by forty-nine and take a look at the digits:

$$5 / 49 = 0.10204081632653061…$$

Do you see a pattern in the digits? Yes! It’s powers of two: (0.)1, 02, 04, 08, 16, 32, 65, … Huh, 65? Yes! The next number, 128, is a three-digit number and so the first digit “overlaps” the last digit of 64, making it 65. And this continues for the first digits of 256 (28 + 2 = 30), 512, the first two digits of 1024, etc. Then floating point errors kicked in, and we stopped there.

I immediately googled it, but no one seems to have noticed this pattern in the digits before. It began to dawn on us that we may just be looking at a hitherto undiscovered “interesting number” such as pi, e, the golden ratio, etc. But the social norms of family meetings do not allow for simulations and mathematical derivations, so we put it aside.

Simulations

The number kept lingering in the back of my head. A few weeks later, I had several pressing deadlines, and as usual, procrastination kicked in full force. I needed to see how far this sequence continued. I fired up Python and wrote a small script which generates the power sequence first, then calculates the number 5/49, and finally identifies at what decimal place the two diverge:

# Power of two to evaluate up to
max_power = 20

# Generate the perfect 102040... sequence in integers instead of decimals
# to avoid floating point errors
power_decimals = 0
for i in range(max_power+1):
    trailing_zeroes = 10**(max_power*2 - i*2)
    power_decimals += trailing_zeroes * 2**i
    print('0.%41d'  %(trailing_zeroes * 2**i), '2^%i'%i)

power_number = '0.%i' %power_decimals  # Add "0."
print(power_number, 'Power')

# Print 5/49 without floating point errors
from decimal import Decimal, getcontext
getcontext().prec = max_power*2+1
fraction = str(Decimal(5) / Decimal(49))
print(fraction, 'Fraction')

# Compare them digit for digit: when do they diverge?
for i in range(len(fraction)):
    if fraction[i] != power_number[i]:
        print('Identical until decimal %i' %(i - 2))  # Don't count "0." as decimals
        break

The print-function in the first for-loop visualizes the adding of the power sequence:

0.10000000000000000000000000000000000000000 2^0
0.  200000000000000000000000000000000000000 2^1
0.    4000000000000000000000000000000000000 2^2
0.      80000000000000000000000000000000000 2^3
0.       1600000000000000000000000000000000 2^4
0.         32000000000000000000000000000000 2^5
0.           640000000000000000000000000000 2^6
0.            12800000000000000000000000000 2^7
0.              256000000000000000000000000 2^8
0.                5120000000000000000000000 2^9
0.                 102400000000000000000000 2^10
0.                   2048000000000000000000 2^11
0.                     40960000000000000000 2^12
0.                       819200000000000000 2^13
0.                        16384000000000000 2^14
0.                          327680000000000 2^15
0.                            6553600000000 2^16
0.                             131072000000 2^17
0.                               2621440000 2^18
0.                                 52428800 2^19
0.                                  1048576 2^20

and the other print functions compare the “ideal” number to the fraction:

0.10204081632653061224489795918367346917376 Power
0.10204081632653061224489795918367346938776 Fraction
Identical until decimal 36

Ok, wow, so it goes on for quite a while. Setting max_power = 10.000 and…

Identical until decimal 16992

Now I’m convinced that this is an infinite pattern. But it gets even better: the sequence starts over every 42 digits. I repeat: Every. 42!!! Digits. Here are the first 168 decimals:

5/49 = 0.
102040816326530612244897959183673469387755
102040816326530612244897959183673469387755
102040816326530612244897959183673469387755
102040816326530612244897959183673469387755...

Is the key to the universe hidden in there somewhere!!?? I was exploding with excitement when I ran and presented this to my wife late in the evening.

The math

My wife is a mathematician. She was not impressed. “Jonas, do you know how to divide five by forty-nine by hand?”. No, I must admit that I never properly learned to do long division (even though I later enjoyed doing long polynomial division). And sure enough: the remainder of the first operation is 50-49 = 1. The remainder of the second operation is two decimal places further to the right where 1 is 100, and the equation becomes 100 – 98 = 2. Then two further to the right and doubling again: 200 – 196 = 4. Then 400 – 392 = 8, etc.

Every 21 such operations the division again hits the operation 50/49, and it repeats. This is extremely common for integer fractions in general. In fact, all rational numbers either have repeating decimals (like 5/49) or terminate (like 1/4 = 0.250000…), so one should not be surprised. Also, this particular 42-decimal period is shared by the division of 42 different integers by 49, albeit starting at different locations in the sequence, e.g., 1/49=0.02040816… and 3/49=0.06122448….

My wife went to bed. For a few seconds, I felt bad. My intellectual love affair crashed hard upon realizing that 5/49 was in many respects just a normal number. But as with human relationships, so with numbers: I’ve learned a great deal about rational numbers through this journey and that’s a comfort.

Conclusion

I do still think that 5/49 stands out. A 42-decimal period with powers of two is an intriguing property only shared by x/49 fractions. Furthermore, 5/49 is the only one of these fractions to start at 2⁰=1 – the true beginning of the power sequence.

The long-division property can be exploited to generate numbers with custom power-sequences in the decimals. So without further ado, I give you:

$$10/(10^n-x)$$

… where x ∈ R_≥0 is the root of the exponential and n ∈ N_≥2 is the number of decimal places between each number. Let’s try this for a few numbers:

10/(10^4 – 3) = 0.00100030009002700...  # Powers of three with four spaces
10/(10^3 - 2) = 0.01002004008016032...  # Powers of two with three spaces
10/(10^2 - 4) = 0.10416666666666667...  # Powers of four rises too quickly for two spaces
10/(10^3 - pi) = 0.0100315149336198...  # Powers of pi, just for fun.

For two decimal places between powers of two, we get

$$10/(10^2 – 2) = 10/98 = 5/49$$

I hope that this number will henceforth be known as Lindeløv’s number. At least it’s on Google now.

I do not recommend hypnosis for brain injury (yet)

14. November 2017 28. January 2019

Jan 2019 update: Given the latest articles on this and a more extensive literature search, I am now convinced about the effectiveness of hypnosis after brain injury than I was when writing this initially. Still, much of this is lower-quality research than I’d like. So the below is still accurate.

I have been overwhelmed with requests following our article about the effect of hypnotic suggestion on working memory performance following acquired brain injury. I present frequent questions and very short answers below. My answers to the questions all originate in the same point: there is insufficient evidence right now to establish whether to use or not to use hypnosis for the treatment of cognitive problems following acquired brain injury. I predict that we should be able to give a recommendation (or refusal) regarding hypnosis following acquired brain injury in 2020.

Frequent questions from patients and relatives:

Question: I have a brain injury. Where can I get hypnosis?
Answer: I won’t give any recommendations. I am a researcher and there is not a firm research-based basis for such a recommendation. If you choose to find a hypnotist, make sure to avoid hypnotists who offer regression to past lives, healing of aura, contact with dead relatives, etc. They have demonstrated an inability to learn from science.

Question: Can I be a test subject in an experiment?
Answer: Unfortunately, not by asking me. If we had experiments with open recruitment, we would recruit through other sources to avoid the strong selection bias.

Question: My daughter is diagnosed with ADHD/Schizophrenia/chronic pain/other – can hypnosis help her?
Answer: The results from our experiment should not be uncritically transferred to other conditions. I do not know enough about the effectiveness of hypnosis for the condition you mentioned here.

Frequent questions from rehabilitation professionals and hypnotists:

Question: Can you send me the manuscript?
Answer: No, the manuscripts will be made freely available if (and only if) there is sufficient evidence to decide if it can be recommended as a generalized treatment. We expect to have that evidence in 2020. Here is a list of all public information about the our experiment, which is more than for most scientific articles. This includes some excerpts from the manuscript in the supplementary materials.

Question: Can you help us get started using this intervention for our clients?
Answer: I’m eager to work with you to set up a research project if you are an institution working professionally with brain-injured patients. That means that you can offer the treatment but you will have less control over to whom and how the treatment is administered while the research is ongoing. These projects are needed to accumulate the evidence to decide if hypnosis can be recommended as a treatment for cognitive problems following acquired brain injury.

Background to the answers

Although our study is very convincing in and of itself, it is just one study and one should remember to factor in prior skepticism and that skepticism should be quite high in this case. The results are surprising exactly because they seem unlikely given prior evidence. One also should consider the fact that the results from scientific studies on humans and animals often fail to replicate. I know of several widely used “treatments” in neurorehabilitation that was introduced because of positive early studies but they are still lingering on even though the collective evidence points to small or no effects. If our results should fail to replicate, its better that hypnosis was never brought to use in neurorehabilitation than spending everybody’s precious time on something ineffective.

I am personally optimistic because I have more (less scientific) sources of evidence than what has been published, but I am also a strong believer in science as the right way to make clinical recommendations. With the ongoing and planned studies, I expect that we have sufficient evidence to make a recommendation (whether for or against) in 2020. We keep the final details about the intervention to research projects until then.

I may come across as dismissive. I really am both personally moved by individual stories and intellectually baffled by the scale of the problem on a world scale. I believe that the solution above will, on average, be the best. One potential advantage of it is that it increases the probability that the treatment, if effective, will be implemented in standard treatment instead of on the all-too-grey market of private hypnotists.

See also my post on what our experiment did not show.

Jeg anbefaler ikke hypnose efter erhvervet hjerneskade (endnu)

14. November 2017 5. March 2019

Jeg får mange henvendelser omkring vores artikel om effekten af hypnotiske suggestioner på arbejdshukommelsen efter erhvervet hjerneskade. Nedenfor giver jeg korte svar på ofte stillede spørgsmål. Alle svarene bunder i den samme pointe: der er endnu ikke tilstrækkelig evidens til at afgøre, om hypnose kan- eller ikke kan anbefales som behandling af kognitive problemer efter erhvervet hjerneskade. Jeg forventer, at vi kan anbefale (eller afvise) hypnose efter erhvervet hjerneskade omkring år 2020.

Ofte stillede spørgsmål af patienter og pårørende:

Spørgsmål: Kan du anbefale en hypnotisør?
Svar: Jeg vil ikke anbefale nogen. Jeg arbejder med forskning og der er ikke et stærkt nok forskningsbaseret grundlag for at give en anbefaling. Hvis du vælger at opsøge en hypnotisør, så undgå alle der tilbyder regression til tidligere liv, healing af aura, kontakt med døde pårørende osv. De har dermed vist, at de ikke arbejder videnskabeligt.

Spørgsmål: Can jeg være med i et eksperiment?
Svar: Desværre ikke ved at spørge mig. Hvis vi havde eksperimenter der manglede deltagere ville vi rekruttere igennem andre kilder (fx hjerneskadeforeningen og hjernesagen) for at mindske selektionsbias.

Spørgsmål: Kan hypnose hjælpe mod ADHD/Skizofreni/kronisk smerte/andet?
Svar: Resultaterne fra vores eksperiment kan næppe overføres så direkte til andre patientgrupper. Jeg kender ikke nok til hvor effektiv hypnose er på den problematik du nævner til at give et svar.

Ofte stillede spørgsmål af professionelle indenfor rehabilitering og hypnose:

Spørgsmål: Kan du sende mig manuskriptet?
Svar: Nej, manuskripterne gøres frit tilgængelige, hvis (og kun hvis) der er tilstrækkelig med forskning der viser, at det kan anbefales som en generel behandling. Her er en oversigt over al offentlig information omkring vores eksperiment, hvilket er mere end for det meste forskning. Dette inkluderer nogle uddrag fra manuskriptet, som du finder i supplementary materials.

Spørgsmål: kan du hjælpe os i gang med at bruge denne intervention til vores klienter?
Svar: Jeg vil meget gerne samarbejde med jer om at starte et forskningsprojekt hvis I er en institution som arbejder professionelt med borgere med erhvervet hjerneskade. Det betyder, at I får muligheden for at tilbyde det til borgerne, men også at I får mindre kontrol over hvordan det udbydes, mens forskningen pågår. Denne slags forskningsprojekter er nødvendige for at afgøre, om hypnose kan abefales som en behandoling af kognitive problematikker efter erhvervet hjerneskade.

Baggrund for svarene

Selvom vores resultater i ovenstående artikel er meget overbevisende isoleret set, er det stadig kun et enkelt eksperiment. Man skal huske at medregne den skepsis man ville have overfor resultaterne, da de bryder med en del veletableret forskning. Man skal også huske, at resultaterne fra videnskabelige studier på dyr og mennesker ofte ikke kan gentages. Jeg er bekendt med flere udbredte “behandlinger” i neurorehabilitering, som netop blev taget på grund af nogle positive resultater, og som stadig er i brug selvom den samlede evidens nu viser at effekten er meget lille eller helt fraværende. Hvis vores resultater ikke kan gentages, er det bedre at hypnose aldrig blev taget i brug i neurorehabilitering, end at alle bruger deres kostbare tid på noget ineffektivt.

Personligt er jeg optimistisk fordi jeg kender til flere (mindre videnskabelige) resultater end det der er blevet publiceret. Men jeg står også fast på, at videnskab må være det rigtige grundlag for kliniske anbefalinger. Med de igangværende og planlagte studier forventer jeg at vi har nok resultater til at give en egentlig anbefalinger (hvad end den er for eller imod) i år 2020. Indtil da holder vi visse detaljer om metoden lukket til forskningsprojekter.

Jeg kan måske give indtryk af at være afvisende. Jeg er personligt rørt over historierne fra alle de personer med hjerneskade jeg har mødt. Jeg er også intellektuelt oprørt over størrelsen af problemet på verdensplan. Jeg tror at ovenstående strategi vil give det bedste udfald i gennemsnit. En mulig fordel er fx at det øger sandsynligheden for, at behandlingen (hvis den er effektiv) bliver implementeret som en del af den offentlige behandling i stedet for at blive overladt til det grå marked af privatpraktiserende hypnotisører.

Se også min post om hvad vores eksperimnet ikke viser.

Decimals of PI with consistent colors

10. November 2017 31. July 2022 itemprop="discussionURL"0

I was invited to do a fun task by my office colleague, Hazel Anderson. She researches synesthesia, and she wanted to induce grapheme-color synesthesia by having participants learn pi using digit-color mapping as one available strategy. So she needed something that could a Word document with pi with an arbitrary number of decimal places. Approximately 40 minutes of the pure joy of structured procrastination and:

Here’s the python script to generate this beauty:

# Settings here
DIGITS = 5000  # Number of decimal places to print
BLOCK_SIZE = 4  # Number of digits between spaces
BLOCK_SPACING = 4  # Size of space between blocks
GRAPHEME_COLOR_MAPPING = {  # Type in your digit-color mapping
    '0': (128, 128, 255),
    '1': (255, 0, 255),
    '2': (128, 0, 255),
    '3': (0, 128, 255),
    '4': (0, 255, 255),
    '5': (255, 255, 0),
    '6': (100, 255, 0),
    '7': (0, 0, 0),
    '8': (70, 255, 70),
    '9': (255, 128, 128)
}

# Set up document
from docx import Document
from docx.shared import RGBColor
document = Document()
paragraph = document.add_paragraph('')  # Start with an empty text

# Create Pi
from mpmath import mp
mp.dps = DIGITS  # Set number of decimals
pi = str(mp.pi)[2:]  # Get all decimals as (iterable) string

# Add digits to Word document
for i, digit in enumerate(pi):
    # Add spacing between blocks
    if i % BLOCK_SIZE == 0 and i > 0:
        paragraph.add_run(' ' * BLOCK_SPACING)
    
    # Add colored digit
    run = paragraph.add_run(digit)
    run.font.color.rgb = RGBColor(*GRAPHEME_COLOR_MAPPING[digit])

# Save it!
document.save('pi in colors.docx')

Scientific papers on hypnosis and brain injury

30. May 2017 12. November 2020

This is an attempt to make a complete up-to-date list of all literature pertaining to hypnosis and brain injury. I now consider the literature so big and dispersed that I feel quite confident that my list won’t be complete, but hopefully, it can get close. In each section, the most informative paper(s) are highlighted in green font.

This list contains many case-studies so there is likely a strong positive bias. I would advise reading the cases purely for methodological inspiration and look to the more systematic and comprehensive studies for an actual assessment of treatment effects.

I recommend reading the review by Appel (2003) as a start. It is a review on hypnosis for rehabilitation in general (not only brain injury) and is by far the most comprehensive review available so far, citing around half of the papers below.

As a side note, I was completely unaware of the scale of the literature when I undertook this search. The first version of this post contained around 10 papers and I considered it complete. One notable surprise is that the list of researchers now includes Milton Erickson and Aaron T. Beck in addition to John Kihlstrom.

Cognition

Status (April 2018): Completed.

Summary of the literature: There are (large) positive effects of hypnosis on cognition following acquired brain injury.

Cui-ping, L. I. (2011). Influence of hypnosis therapy on recovery of hemorrhagic stroke. Journal of Taishan Medical College, 1, 025. http://en.cnki.com.cn/Article_en/CJFDTOTAL-TSYX201101025.htm (see my English translation and comments)
An RCT showing large effects (SMD = 1.0 to 1.7) on Barthel, anxiety, and depression in stroke patients given ten sessions of hypnosis between one and twelve weeks after the injury onset. The study is relatively large with 120 treatment-as-usual patients of which 49 had additional adjunctive hypnosis. It was published in Chinese in a Chinese journal with impact factor 0.1, and it is unclear whether it was peer-reviewed. In general, there are many reasons to be skeptical of the quality of this paper. Nonetheless, everything else being equal, it does increase the probability that hypnosis can improve cognition following acquired brain injury. With the help of Chinese friends, I got hold of the paper and helped reading it. I’ve added a link to my translation in the reference above, containing comments to clarify particular unclear sections and dubious statistics
Lindeløv, J. K., Overgaard, R., & Overgaard, M. (2017). Improving working memory performance in brain-injured patients using hypnotic suggestion. Brain, 140(4), 1100–1106. https://doi.org/10.1093/brain/awx001.
Our study, showing a large specific effect on working memory performance of hypnotic suggestions involving the return to pre-injury (or normal) functioning. It’s an RCT with a total of 68 patients stratified to targeted hypnosis, an active control, and a passive control. The effect of four and eight treatment sessions is assessed with long-term follow-up.
Milos, R. (1975). Hypnotic exploration of amnesia after cerebral injuries. International Journal of Clinical and Experimental Hypnosis, 23(2), 103–110. https://doi.org/10.1080/00207147508415934
This paper is not really on cognitive rehabilitation but it does manage to (temporarily) get retrospective reports of experiences that were otherwise inaccessible due to retrograde or anterograde amnesia during hypnosis in 7 out of 20 cases of severe injury. It was not checked whether these reports were accurate, so this is prone to confabulations or changes in response criterions rather than a true cancellation of amnesia.
Sullivan, D. S., Johnson, A., & Bratkovitch, J. (1974). Reduction of behavioral deficit in organic brain damage by use of hypnosis. Journal of Clinical Psychology, 30(1), 96–98. https://journals.lww.com/actjournalonline/Abstract/2007/10000/Alternative_Approaches_to_Supporting_Individuals.8.aspx
Later we discovered this similar study had been carried out by Sullivan et al. (1974). The Sullivan study, however, had an intervention consisting of just seven sentences repeated twice – probably less than two minutes! They obtained a small positive effect on the Picture Completion task from the WAIS battery but not on the Binder-Gestalt test. They had a quite small sample, and the two-page article leaves many details unreported.
Vanhaudenhuyse, A., Laureys, S., & Faymonville, M.-E. (2015). The use of hypnosis in severe brain injury rehabilitation: a case report. Acta Neurologica Belgica, 115(4), 771–772. https://doi.org/10.1007/s13760-015-0459-3
A brief report on a 50-year case with cerebral hemorrhage, who underwent hypnosis when he was deemed chronic with severe symptoms. Hypnosis sparked further improvement. As a side note, the authors write that “To the best of our knowledge, this is the first study reporting on the integration of hypnosis as part of rehabilitation treatment of severe brain injury patients.” Well… 🙂

Motor disorders

Status (April, 2018): Approximately 70% completed. Needs a search for post-2000 literature, references, and citations

With the notable exception of Spankus & Freeman (1962) and Irawan et al. (2018), this literature consists largely of single-case studies, making it very vulnerable to publication bias. Confirming this, most studies report positive findings while Spankus & Freeman (1962) only report positive outcomes for four out of nineteen patients with cerebral palsy. Although somewhat disconcerting, this observation may not generalize to all of the literature given the large variability in the patient characteristics and treatment protocols between papers.

Alexander, L. (1966). Hypnosis in primarily organic illness. American Journal of Clinical Hypnosis, 8(4), 250-253.
Appel, P. R. (1990). Clinical Applications of Hypnosis in the Physical Medicine and Rehabilitation Setting: Three Case Reports. American Journal of Clinical Hypnosis, 33(2), 85–93. https://doi.org/10.1080/00029157.1990.10402909
See case number two.
Chappell, D. T. (1961a). A Psychological Approach to Traumatic Paraplegia: Use of Hypnosis. The Journal of Nervous and Mental Disease, 132(5), 432.
Chappell, D. T. (1961b). The Reduction of Spasticity in Paraplegia with Hypnosis. American Journal of Clinical Hypnosis, 3(4), 213–225. https://doi.org/10.1080/00029157.1961.10401844
Chappell, D. T. (1964). Hypnosis and Spasticity in Paraplegia. American Journal of Clinical Hypnosis, 7(1), 33–36. https://doi.org/10.1080/00029157.1964.10402388
Crasilneck, H. B., & Hall, J. A. (1970). The use of hypnosis in the rehabilitation of complicate vascular and post-traumatic neurological patients. International Journal of Clinical and Experimental Hypnosis, 18(3), 145–159.
Diamond, S. G., Davis, O. C., Schaechter, J. D., & Howe, R. D. (2006). Hypnosis for rehabilitation after stroke: six case studies. Contemporary Hypnosis, 23(4), 173–180. https://doi.org/10.1002/ch.319
Holroyd, J., & Hill, A. (1989). Pushing the limits of recovery: Hypnotherapy with a stroke patient. International Journal of Clinical and Experimental Hypnosis, 37(2), 120–128. https://doi.org/10.1080/00207148908410541
Irawan, C., Mardiyono, M., Suharto, S., & Santjaka, A. (2018). COMBINATION OF HYPNOSIS THERAPY AND RANGE OF MOTION EXERCISE ON UPPER-EXTREMITY MUSCLE STRENGTH IN PATIENTS WITH NON-HEMORRAGHIC STROKE. Belitung Nursing Journal, 4(1), 104-111.
This is an RCT on 2 x 16 stroke patients. Although the descriptive statistics seem convincing, there are some red flags. For example, the journal seems a bit dubious, there are spelling/grammatical mistakes, and half of the citations are non-English. More content-related, the statistics are relatively poor, lacking the test of the crucial 2 (pre/post) x 2 (treatment/control) interaction term, which would be identical to the independent t-test on the change scores in each group. It does look like such a test would come out significant with a test would come out positive given the large improvement in the treatment group (d = 1) as compared to the control group (d = 0.1).
Manganiello, A. J. (1986). Hypnotherapy in the rehabilitation of a stroke victim: a case study. The American Journal of Clinical Hypnosis, 29(1), 64–68. https://doi.org/10.1080/00029157.1986.10402680
Mauersberger, K., Artz, K., Duncan, B., & Gurgevich, S. (2000). Can children with spastic cerebral palsy use self-hypnosis to reduce muscle tone? a preliminary study. Integrative Medicine, 2(2), 93–96. https://doi.org/10.1016/S1096-2190(00)00008-1
Martin, J. (1983). Hypnosis also useful in rehabilitation therapy. JAMA, 249(12), 1536–1536. https://doi.org/10.1001/jama.1983.03330360006002
Radil, T., Snýdrová, I., Háĉik, L., Pfeiffer, J., & Votava, J. (1988). Attempts to influence movement disorders in hemiparetics. Scandinavian journal of rehabilitation medicine. Supplement, 17, 157-161.
Safitri, K. H., Irawaty, D., & Masfuri, M. (2018). Effect Hypnotherapy for Increasing Muscle Strength in Stroke Patient with Hemiparesis. International Journal of Nursing, Health and Medicine, 1(1), 7–13. All alarms go off with this paper. An unknown journal, major grammatical errors (bordering on not being comprehensible), and major omissions in the reporting. Still, it’s a controlled study with 44 hemmorrhagic stroke patients, so it has larger weight than many other studies on this list. Says that “No publication of research like this before” which is obviously false, as is apparent from this list.
Seder, I. I., & Gelberd, M. B. (1964). Hypnosis as a Relaxant for the Cerebral Palsied Patient. American Journal of Clinical Hypnosis, 6(4), 364–365. https://doi.org/10.1080/00029157.1964.10402378
Slater, R. C., & Flores, L. S. (1963). Hypnosis in organic symptom removal: A temporary removal of an organic paralysis by hypnosis. American Journal of Clinical Hypnosis, 5(4), 248-255.
Spankus, W. H., & Freeman, L. G. (1962). Hypnosis in cerebral palsy. International Journal of Clinical and Experimental Hypnosis, 10(3), 135–139. https://doi.org/10.1080/00207146208415875
Vodovnik, L., Roskar, E., Pajntar, M., & Gros, N. (1979). Modeling the voluntary hypnosis-induced motor performance of hemiparetic patients. IEEE Trans. on Systems, Man, and Cybernetics, SMC-9 (12).
Yensen, R. (1963). Hypnosis and Movement Re-Education in Partially Paralysed Subjects. Perceptual and Motor Skills, 17(1), 211–222. https://doi.org/10.2466/pms.1963.17.1.211

Citations without available abstract or full text below. Notice that the list includes papers on neuromuscular illnesses, even though these typically relate to the peripheral nerve system. But due to my inability to scan these papers, I keep them on the list in case they include cases of brain injury.

Baer, R. F. (1962). Hypnosis in the treatment of neuromuscular sequelae of injuries. Industrial medicine & surgery, 31, 315.
Kroger, W.S. (1970) Hypnosis therapy in neuromuscular disorders. Osteopathic Physician (1970), pp. 69-70, September.
Martin (1983, see above) cites a paper by Korn which I cannot find, saying: “At least Errol R. Korn, MD, can point to definite rehabilitative gains made by “dozens of patients” with stroke and spinal cord injuries in relearning the swallowing reflex, regaining muscle and balance control, and healing decubitus ulcers.”
Ortega DF (1978). Relaxation exercise with cerebral palsied adults showing spasticity. J Appl Behav Anal 11(4):447-451
E. Roskar, M. Pajntar, L. Vodovnik, and N. Gros (1977) Improvements of motor response in hemiplegic patients by means of hypnosis, in Proc. I st. Mediterranean Conf. on Med. and Biol. Engng., Sorrento, Italy, pp. 1-85-I-88.
E. Roskar, M. Pajntar, L. Vodovnik, and N. Gros (1978.) Improved neuromuscular activity of hemiparetic extremity due to hypnosis, Advances in External Control of Human Extremities, Yugoslav Committee for Electronics and Automation, Belgrade, pp. 257-268
Secter IL, Gilberd MB (1964). Hypnosis as a relaxant for the cerebral palsied patient. Am J Clin Hypn 6:363-364.
Shires EB, Peters JJ, Krout RM (1954) Hypnosis in neuromuscular re-education. U.S. Armed Forces Medical Journal 5: 1519–23.

Aphasia

Status (April 2018): Completed.

Kirkner, F. J., Dorcus, R. M., & Seacat, G. (1953). Hypnotic motivation of vocalization in an organic motor aphasic case. Journal of Clinical and Experimental Hypnosis, 1(3), 47–49. https://doi.org/10.1080/00207145308411081
Laures, J. S., & Shisler, R. J. (2004). Complementary and alternative medical approaches to treating adult neurogenic communication disorders: a review. Disability and Rehabilitation, 26(6), 315–325. https://doi.org/10.1080/0963828032000174106
Contains a very short section (page 317-318) reviewing Thompson et al. (1986) and Manganielly (1986) (see this list). Finds the results promising but insufficient due to weaknesses from inconsistency in the former and lack of objective outcome measures in the latter.
Macfarlane, F. K., & Duckworth, M. (1990). The use of hypnosis in speech therapy: a questionnaire study. British Journal of Disorders of Communication, 25(2), 227-246.
This is just a survey on usage frequencies without an assessment of effectiveness. Also covers non-neurological speech problems.
Mason, C. F. (1961). Hypnotic motivation of aphasics. International Journal of Clinical and Experimental Hypnosis, 9, 297–301. https://doi.org/10.1080/00207146108409683
McKeever, W. F., Larrabee, G. J., Sullivan, K. F., Johnson, H. J., Furguson, S., & Rayport, M. (1981). Unimanual tactile anomia consequent to corpus callosotomy: Reduction of anomic deficit under hypnosis. Neuropsychologia, 19(2), 179–190. https://doi.org/10.1016/0028-3932(81)90103-2
Moss, C. S. (1972). Recovery with aphasia: The aftermath of my stroke. Oxford, England: U. Illinois Press.
This is a self-report (i.e., not a scientific paper) of a clinical neuropsychologist who suffered from aphasia following a cerebral vascular incident. Moss recovered well and reports, among other things, on hypnotherapy in the process.
Thompson, C. K., Hall, H. R., & Sison, C. E. (1986). Effects of hypnosis and imagery training on naming behavior in aphasia. Brain and Language, 28(1), 141–153. https://doi.org/10.1016/0093-934X(86)90097-0

Citations without available abstract or full text:

GILDSTON, H., & GILDSTON, P. (1986, January). HYPNOTHERAPY IN ADULT APHASIA REHABILITATION. In FOLIA PHONIATRICA (Vol. 38, No. 5-6, pp. 301-301). ALLSCHWILERSTRASSE 10, CH-4009 BASEL, SWITZERLAND: KARGER.
Glazer, M. J. (1964). A comparison of performance of predominantly expressive aphasic patients before, during and after hypnosis: a thesis (Doctoral dissertation, Tulane University).
HONEYGOSKY, R. (1976, January). APPLICATION OF RELAXATION THERAPY, AUTOGENIC THERAPY, BIOFEEDBACK, AND HYPNOSIS IN REHABILITATION OF CERTAIN FORMS OF APHASIA. In FOLIA PHONIATRICA(Vol. 28, No. 4-5, pp. 243-243). ALLSCHWILERSTRASSE 10, CH-4009 BASEL, SWITZERLAND: KARGER

Dementias

Status (April, 2018): Approximately 50% completed. Needs a systematic search, reference search, and citation search.

Eisenberg, M. G., & Jansen, M. A. (1983). Rehabilitation psychology: State of the art. Annual review of rehabilitation.This review contains a quite extensive section on hypnosis for dementias. Though this is superseded by Appel the (2003) review
Duff, S., & Nightingale, D. (2007). Alternative Approaches to Supporting Individuals With Dementia: Enhancing Quality of Life Through Hypnosis. Alzheimer’s Care Today, 8(4), 321. https://doi.org/10.1097/01.ALCAT.0000297153.89903.7bThis is an RCT with a treatment group, an active control group (discussion groups) and a treatment-as-usual group. The participants were recruited from care homes and had vascular dementia (acquired brain injury) or dementia (unspecified…), and a few Parkinson’s patients. The intervention was quite extensive with 36 weekly sessions of hypnosis or discussion and a 12-month follow-up after that. The outcome was a questionnaire-only assessment of Quality of Life with large effects on all aspects which were all maintained after 12 months, except for relaxation. The small sample size and the subjective nature of the report are reasons to be cautious, but otherwise, it’s some of the most informative data on hypnosis for dementias to date (2018).
Palmieri, A., Kleinbub, J. R., Calvo, V., Sorarù, G., Grasso, I., Messina, I., & Sambin, M. (2012). Efficacy of hypnosis-based treatment in amyotrophic lateral sclerosis: a pilot study. Frontiers in psychology, 3, 465.https://doi.org/10.3389/fpsyg.2012.00465 A small sample of 8 ALS patients was treated using Ericksonian hypnosis during four weekly 45-minute sessions. A CD with the hypnotic induction was offered for daily home use. The effect sizes on (self-reported) depression, anxiety, and quality-of-life was beyond-large (cliff’s delta around 0.75) in general with some larger and some smaller. There were similar effects on relative-reported caregiver burden. While this study is stronger than case studies (eight times stronger?), the lack of control likely means that these effects are likely overestimated.
Elkins, G., Sliwinski, J., Bowers, J., & Encarnacion, E. (2013). Feasibility of clinical hypnosis for the treatment of parkinson’s disease: a case study. International Journal of Clinical and Experimental Hypnosis, 61(2), 172-182. https://doi.org/10.1080/00207144.2013.753829 Almost complete removal of tremor in a parkinson patient following three weekly hypnosis sessions. It’s hard to know from this case how well this generalizes, or whether there was something special (read: unrepresentative) about this patient.
Stambaugh, E. E. (1977). Hypnotic treatment of depression in the Parkinsonian patient: A case study. American Journal of Clinical Hypnosis, 19(3), 185-186. https://doi.org/10.1080/00029157.1977.10403869

Not properly vetted for this list yet (copy-pasted from Appel (2003)):

H.J. Wain, D. Amen, B. Jabbari The effects of hypnosis on a Parkinsonian tremor: Case report with polygraph/EEG recordings.
Am J Clin Hypn, 33 (1990), pp. 94-98
F.A. Buell, J.P. Biehl The influence of hypnosis on the tremor of Parkinson’s disease
Journal of Disorders of the Nervous System, 10 (1949), pp. 20-23
H.W. Bird Varying hypnotizability in a case of Parkinsonism
Bull Menninger Clin, 12 (1948), pp. 210-217
M. Witz, S. Kahn Hypnosis and the treatment of Huntington’s Disease
Am J Clin Hypn, 34 (1991), pp. 79-90
R. Moldawsky Hypnosis as an adjunctive treatment in Huntington’s disease
Am J Clin Hypn, 26 (1984), pp. 229-231
V. Stein Hypnotherapy of involuntary movements in an 82-year-old man
Am J Clin Hypn, 23 (1980), pp. 128-131
D. Vann Successful hypnotherapy for anxiety neuroses in Huntingtonı́s chorea
Med J Aust, 2 (1971), p. 166
G. Ambrose Multiple sclerosis and treatment by hypnotherapy
Am J Clin Hypn, 3 (1955), pp. 203-209
R.F. Baer Hypnosis, An adjunct in the treatment of neuromuscular disease
Arch Phys Med Rehabil, 41 (1960), pp. 514-515
J.T. Brunn Hypnosis and neurological disease: A case report
Am J Clin Hypn, 8 (1966), pp. 312-313 (Link)
J.R. Dane Hypnosis for pain and neuromuscular rehabilitation with multiple sclerosis: Case summary, literature review, and analysis of outcomes
Int J Clin Exp Hypn, 44 (1996), pp. 208-231
H. McCord Hypnotically hallucinated physical therapy with a multiple sclerosis patient
Am J Clin Hypn, 5 (1963), p. 168
H. McCord Hypnosis and multiple sclerosis: A brief case report
Am J Clin Hypn, 8 (1966), pp. 313-314
D.Y. Medd The use of hypnosis in multiple sclerosis: Four case studies
Contemp Hypn, 9 (1) (1992), pp. 62-66
B. Strauss, S. Billie Hypnosis with cerebral palsy patients, and how may it be applied
ASCH Newsletter, 26 (6) (1985), p. 2
R.F. Baer Hypnosis applied to bowel and bladder control in multiple sclerosis, syringomelia and traumatic transverse myelitis
Am J Clin Hypn, 4 (1961), pp. 22-23
Also check out other papers by Duff. For example, is this a fulltext? Are they merely reporting the same results as Duff (2007) at earlier stages?

Pain, vertigo, anxiety (in progress)

Status (April, 2018): Approximately 40% completed. Needs a systematic search, reference search, and citation search.

This is a catch-all category for directly unpleasant sequelae following acquired brain injury. Sullivan et al. (1974) hypothesized that they relieved anxiety. But they never directly assessed anxiety, so I presented it on the list for cognitive rehabilitation. Fromm (1964) and Gruenewald & Fromm (1967) tried to induce catastrophic anxiety in healthy subjects.

Cedercreutz, C., Lähteenmäki, R., & Tulikoura, J. (1976). Hypnotic treatment of headache and vertigo in skull injured patients. International Journal of Clinical and Experimental Hypnosis, 24(3–4), 195–201. https://doi.org/10.1080/00207147608416201
This paper summarizes clinical results of 155 patients with pain and/or vertigo sequelae. So this is a large portion of evidence as compared to the rest of this list. As with the other case studies, it may be prone to experimenter bias. The reported effects are quite impressive in a median of three-to-four sessions to achieve complete symptom relief in more than half of the patients.
Laclave, L. J., & Blix, S. (1989). Hypnosis in the management of symptoms in a young girl with malignant astrocytoma: A challenge to the therapist. International journal of clinical and experimental hypnosis, 37(1), 6-14.
A single-case study on a 6½-year old girl predominantly focused on nausea following chemotherapy. I still include it on this list because of the neurogenic nature of the disease.
Moss, D. (2018). I hurt so: hypnotic interventions and palliative care for traumatic brain injury. Annals of Palliative Medicine, 7(1), 151–158. https://doi.org/10.21037/apm.2017.08.16
Case study with a TBI patient. Hypnosis for pain and anxiety.
Sapp, M. (1992). Relaxation and hypnosis in reducing anxiety and stress. Australian Journal of Clinical Hypnotherapy and Hypnosis, 13(2), 39-55. Stuff
Bertoni, F., Bonardi, A., Magno, L., Mandracchia, S., Martinelli, L., Terraneo, F., & Tonoli, S. (1999). Hypnosis instead of general anaesthesia in paediatric radiotherapy: report of three cases. Radiotherapy and oncology, 52(2), 185-190.
Two cases of child patients with resected cerebellar tumors undergoing hypnotically induced general anesthesia.
Nolan, M. (2008). Hypnosis to enhance time limited cognitive-behaviour therapy for anxiety. Australian Journal of Clinical and Experimental Hypnosis, 36(1), 30-40.
I was in doubt whether to include this on the list. It is the case of hypnosis with a client who self-reports transient ischemic attacks and fears a full-blown stroke, but there no direct evidence is reported for either. She did have high blood pressure and was subjected to bypass and other treatments.

Suggestibility

Status (April 2018): Completed.

Take-home: Brain injured patients are as suggestible/hypnotizable as the general population

Laidlaw, T. M. (1993). Hypnosis and Attention Deficits After Closed Head Injury. International Journal of Clinical and Experimental Hypnosis, 41(2), 97–111. https://doi.org/10.1080/00207149308414541
No difference in suggestibility on the HGSHS:A for young concussion patients relative to healthy controls.
Lindeløv, J. K., Overgaard, R., & Overgaard, M. (2017). Improving working memory performance in brain-injured patients using hypnotic suggestion. Brain, 140(4), 1100–1106. https://doi.org/10.1093/brain/awx001
Our study tested 49 brain-injured patients on SHSS:C but did not compare them directly to healthy controls. However, looking at SHSS:C norms from other countries, the suggestibility of the patients seemed normal.
Kihlstrom, J. F., Glisky, M. L., McGovern, S., Rapcsak, S. Z., & Mennemeier, M. S. (2013). Hypnosis in the right hemisphere. Cortex, 49(2), 393–399. https://doi.org/10.1016/j.cortex.2012.04.018
No difference in suggestibility between middle-aged stroke patients relative to young controls on AMSH.

General reviews

Status (April 2018): Completed.

Appel, P. R. (2003). Clinical hypnosis in rehabilitation. Seminars in Integrative Medicine, 1(2), 90–105. https://doi.org/10.1016/S1543-1150(03)00010-3
This is an impressive review of the field. For brain injury and neurological conditions, pages 96-97 are particularly relevant.
Appel, P. R. (2003) Clinical Hypnosis. In S. Wainapel, & A. Fast (Eds.) Alternative Medicine and Rehabilitation: A guide for practitioners. NY: Demos
This is basically a shortened version of the excellent other Appel (2003) review. Pages 224-227 are especially relevant for neurological cases.
Wainapel, S. E., & Fast, A. (2002). Alternative Medicine and Rehabilitation: A Guide for Practitioners (1 edition). New York: Demos Medical.
There is a short review on hypnosis for rehabilitation of motor dysfunction, aphasia, etc. on page 225-227. Most, if not all, of the cited literature by Weinapel is on the present list.

Citations without available abstract or full texts:

Wright, M. E. (1960) Hypnosis and rehabilitation. Rehabilit. Lia, 21(1), 2-12.
LaScolla, R. (1975). Hypnosis in stroke rehabilitation. In Scientific Proceedings of the 22nd Annual Meeting of the Am Society of Clinical Hypnosis.
Feher, T.L. (1987) Hypnosis in clinical neurology. In W. Wester (Ed.), Clinical Hypnosis: A Case Management Approach, Behavioral Science Center Inc. Publications, Cincinnati, OH
Celinski, M.J. (1992) Hypnosis in neurological rehabilitation. In W. Bongartz (Ed.), Hypnosis: 175 years after Mesmer-Recent developments in theory and application, Universitaetsverlag, Konstanz, Germany, pp. 357-362
Halama, P. (1993). Hypnotherapy for stroke patients. Hypnos, 20(3), 154-162.
Spellacy, F. (1992). Hypnotherapy following traumatic brain injuries. Hypnos, 19(1), 34-39.

Papers not fitting into the above categories

Gravitz, M. A. (1981). Non-verbal hypnotic techniques in a centrally deaf brain-damaged patient. International Journal of Clinical and Experimental Hypnosis, 29(2), 110-116.
Erickson, M. H. (1963). Hypnotically Oriented Psychotherapy in Organic Brain Damage. American Journal of Clinical Hypnosis, 6(2), 92–112. https://doi.org/10.1080/00029157.1963.10402329
A case of hemiparesis, aphasia, and hyperalgesia following some vascular anomalities. This is Milton Erickson! After 11-months of no progress, Erickson takes on therapy in (at least) five months. There was great progress in this time, though it is not self-evident that this can be attributed to the intervention given the extensive duration of the intervention. His strategy relies heavily on frustrating the patient including lying, overruling, deceiving, etc. in front of others. I personally find his approach appalling. There is very little formal hypnosis in this paper.
Beck, A. T., & Guthrie, T. (1956). Psychological Significance of Visual Auras: Study of Three Cases with Brain Damage and Seizures. Psychosomatic Medicine, 18(2), 133–142. (link to PDF)
Epilepsy following acquired brain injury. Hypnosis was employed in two cases to reveal painful emotional memories connected to the aura. Yes, Aaron T. Beck, the father of cognitive behavioral therapy (CBT) did a study on hypnosis and acquired brain injury!
Mittenberg, W., & Burton, D. B. (1994). A survey of treatments for post-concussion syndrome. Brain Injury, 8(5), 429–437. https://doi.org/10.3109/02699059409150994
Simply shows the result of a survey, that 5.1 % (around 7 out of 165) of therapists use hypnotherapy for post-concussion patients. This is the only mention of hypnosis in the article.

Brain injury “models” in non-injured humans

Status (April 2018): Probably completed. But needs systematic search, reference search, citation search.

Take-home: healthy subjects can be hypnotized to play the role of brain-injured patients, but they are probably not realistic brain-injury models.

Fromm, E., Sawyer, J., & Rosenthal, V. (1964). Hypnotic simulation of organic brain damage. The Journal of Abnormal and Social Psychology, 69(5), 482. http://psycnet.apa.org/index.cfm?fa=buy.optionToBuy&id=1965-08145-001
Hypnotized subjects (n=9) to believed that they had sustained an organic brain injury. After “hypnotic brain injury,” the subjects who experienced being in deep hypnosis were judged to be more “organic” by blinded neuropsychologists than under “hysterical” and no-hypnosis conditions, in which they were judged to be non-injured. The results from this study failed to replicate in a methodologically superior follow-up in Gruenwald & Fromm (1967).
Gruenewald, D., & Fromm, E. (1967). Hypnosis, simulation, and brain damage. Journal of Abnormal Psychology, 72(2), 191–192. https://doi.org/10.1037/h0024452
Replication of Fromm et al. (1964) with an improved method, controlling for more potential confounders. There were no difference between the hypnosis and control group judgment, actual score, or subjective experience.
Wagstaff, M., Parkes, M., & Hanley, J. R. (2001). A comparison of posthypnotic amnesia and the simulation of amnesia through brain injury. International Journal of Psychology and Psychological Therapy, 1(1), 67–78. http://www.ijpsy.com/volumen1/num1/5.html
Like Fromm (1964), but adds malingering-detection tests to the test battery, showing that “hypnotically brain injured” healthy subjects indeed do act as malingerers, not as real brain-injured patients.

Search strategy and current status of this list

Google Scholar was searched using the term “hypnosis OR “hypnotic suggestion” brain-injury OR brain-damage OR stroke OR hemiplegia OR paraplegia OR “traumatic brain” OR “diffuse axonal” OR hemorrhage”. The reference list of all hits for which I had access to full texts were scanned. For some papers, the list of papers citing that paper were scanned too, using Google Scholar.

Next steps (my to do):

Read Appel (2003) thoroughly again for more keywords to search on.
Make a histogram of publication years relative to general science publication volume.
Do searches on post-concussion syndrome?
Dementias? start with this Duff search.

Identified papers that I need to screen/comment:

Look into https://www.amazon.com/Clinical-Experimental-Hypnosis-Dentistry-Psychology-ebook/dp/B01MXFB423. Apparently contains something on hypnosis and brain injury
https://www.frontiersin.org/articles/10.3389/fpsyg.2012.00465/full
Appel PR: Performance enhancement in physical medicine and rehabilitation. Am J Clin Hypn 35:11-19, 1992

Highlight these as best-quality (not necessarily “very good”!) publications in their field:

Lindeløv
Irawan
Duff
Cedercreutz
Laidlaw
Appel (2003)
Wagstaff

Hypnosis and brain injury: where to find stuff

27. January 2017 24. March 2022

This post is a continually updated list of important communications on research following our paper in Brain entitled “Improving working memory performance in brain-injured patients using hypnotic suggestion.”

Scientific reports

All my/our articles have associated free data and analysis. I encourage everyone to scrutinize this, e.g., with alternative analyses, and let me know what you conclude. Please notice that a pre-print is the author’s manuscript before peer-review. So it may have weaknesses that will be corrected through peer-review. Sometimes, peer review also obscures it a bit, so there are pros and cons.

The scientific article in Brain: Argues that targeted hypnotic suggestion improves working memory for people with acquired brain injury. A free version is available here. The supplemental materials (15 pages) include excerpts from the hypnosis script.
Preprint with analyses of interview-data from the article above. Indicates that the improvements are more generalized, including sleep and self-defined goals. It is currently in review at Neuropsychological Rehabilitation (Jan 2019).
Pre-print on patients on Mild Traumatic Brain Injury (concussion) specifically. Large positive effects on fatigue, and positive effects on anxiety and depression. This study lacks a control group so it is lower in the evidential hierarchy.
Pre-print with some interesting cases and a few theoretical considerations which result in three predictions.

My blogs with further info

A list of published scientific literature on hypnosis and brain injury. Three papers support the positive effect of hypnosis on cognitive sequelae following acquired brain injury. Many more have been published on motor rehabilitation, aphasia, pain, dementia, etc.
An anti-hype blog post: Anticipates some potential overinterpretations by the general public (particularly journalists, therapists, and patients) and counter them.
Answers to frequently answered questions by patients, relatives and rehabilitation professions: English and Danish.

Press and public dissemination

Spot on Danish national television, including a case with a 19-year old man who had sustained a traumatic brain injury in a high-speed car crash two years before enrollment in the experiment. The spot is accompanied by two articles and a radio spot (also Danish). Our impression is that this case is in the top 30% on real-life improvement, i.e. not too unrepresentative.
Oxford University Blog: A summary for the general public. It includes a back-of-the-envelope estimation of how much you should update your belief based on this study alone.
This study has been featured in multiple Danish papers, but this contains no new information that isn’t contained in the above. See my press appearances here.

Can I get the manuscript / are new studies ongoing?

Read excepts from the manuscript here and here.

We plan to make the hypnosis scripts available to everybody eventually. On the other hand, we want to avoid putting it “out in the wild” if it somehow turns out to be a fluke. So for now, we pursue a strategy where we only make non-published details about the intervention and the hypnosis scripts available to institutions/companies who can and will evaluate the effectiveness of the scripts systematically.

If you’re such an institution, we’d be eager to set up a collaboration. For example, Tryg Foundation just funded an RCT at Jobkompagniet Silkeborg which will include 90 patients. The first results are expected to be published around December 2022 with an additional report in the summer of 2023. The design and outcome measures simultaneously satisfy research purposes and Jobkompagniet’s core mission.

We expect to stick to this institution-and-evaluation-only strategy for a few years until enough evidence has accumulated that we feel confident about the clinical effectiveness of hypnosis following acquired brain injury. If you’re a private therapist, if you have suffered an acquired brain injury, or if you’re a relative, we will ask you to wait until we have this evidence. Also, see FAQ and answers in the previous section.

What our paper on hypnosis following brain injury does not show

27. January 2017 14. November 2017

We just published a paper in Brain entitled “Improving working memory performance in brain-injured patients using hypnotic suggestion.” We argue that for patients with acquired brain injury, hypnotic suggestion which asks the patient to recover an ability to concentrate and remember improves working memory performance. I also reported the study and the results at the Oxford University Press blog, including an estimate of how skeptical you should be. We expect quite some publicity – and perhaps even hype – around the results of this paper.

Hype and overinterpretation work for advertising but not for science. In this post, I will try to counter some potential misunderstandings. We are incredibly excited about our findings. We just want to make sure that the public is excited for the right reasons and at the right level. As I argued on the OUP blog post, the appropriate state of belief is probably that of a “pessimist turned hopeful” who awaits further data to decide whether to leave the pessimistic stance or keep it. Given that brain injury constitutes the second- and third-largest health-related cost in the world, even a small hope is quite substantial.

Before I continue, I want to highlight that this research was a joint effort by Professor Morten Overgaard, hypnotist Rikke Overgaard, and me. The project was funded by the European Research Council and the Karen Elise Jensen Foundation and organized under Cognitive Neuroscience Research Unit at Center for Functionally Integrative Neuroscience and Aalborg University. The following reflect the views of all authors.

This study does not show that subjects were “cured”

The participants in our study improved to the population average in measures of working memory, which is an important but not all-encompassing cognitive function. We did not assess other domains such as psychological trauma, physical impairment, etc. because we did not target the hypnosis at these domains and therefore it was not part of the research question. Therefore, we cannot make any data-based claims about the effect of hypnosis on those domains.

Hypnosis does not involve anything “mystic” or otherwise “out of this world”

On the gray market of hypnotists, it is all too common to see the same persons offering regression to previous lives, contact with the dead, healing auras, etc. As a scientist, I reject this. In our experiment, the hypnotist sat in a chair and read aloud from a piece of paper. The patient sat in another chair and listened. There’s only a vibrating vocal chord, sound moving through the air, hitting the eardrums of the patient, and then sensory transduction to action potentials in the brain. From there, we strongly expect that the mechanism underlying the effect will eventually be identified among the on-shelf phenomena in psychology and neuroscience, e.g. neural plasticity working bottom-up, unlearning learned non-use, using a different strategy/realization of the same surface behavior, etc. The only novelness of our findings, if they replicate, would then be that these mechanisms apply to brain injury with a large effect size. There’s a long and serious research history on hypnosis in the top neuroscience journals by top researchers. See e.g. this 2013-paper in Nature Reviews Neuroscience by Oakley & Halligan. This is the line of research we are continuing, and it is very different from the current public perception of what hypnosis is.

The cognitive consequences following acquired brain injury are not unreal or hypocrisy

Some may say “if it’s that easy to recover, then it wasn’t a real problem” and perhaps even put the patient at fault. I hope you would agree with me that such a claim would be straight up ridiculous. First, such a claim would entail a psychology-only understanding of brain injury, and since we do now know the mechanism of why hypnotic suggestion works, this remains an open question. Second, even if it turns out that the cognitive impairment following acquired brain injury somehow can be described in purely psychological terms, this does not change the seriousness of the condition. PTSD is not less severe or hypocrisy because it has a psychogenic origin.

No direct evidence of clinical effectiveness (yet)

Neuropsychological test have surprisingly low predictive value for the ability to participate in society, e.g. returning to work, living independently, etc. which is often the primary criterion of clinical success in rehabilitation (sorry, psychologists!) We did not assess the latter directly, but we plan to this in an in-progress follow-up experiment. However, we do have anecdotal evidence that targeted hypnotic suggestion could be effective for participation. Many of the patients returned to us with reports of getting jobs, beginning or finishing education, not getting exhausted from grocery shopping and family parties, etc. This effect was immediate for some and slower for others. I recall one case where the patient only realized that there had been an improvement when the spouse pointed to very tangible evidence such as no more bruises from inattentively walking into stuff. Similarly, an independent psychologist was inspired by our findings and used hypnosis on two brain injured clients with excellent clinical results. But these reports are prone to selection bias (only the positive cases report back) and neglecting base-rate improvements (some would have improved anyway). We need direct evidence on clinical effectiveness, and we don’t have that now.

No direct evidence that hypnosis drives the effect (yet)

In casual talk, it’ll be easy to say that “hypnosis improved working memory.” We even do this ourselves. However, it does not follow directly from our design since both the targeted suggestion procedure and our non-targeted (intended as placebo) suggestion procedure was administered under hypnosis. We did not deliver the same treatment in a non-hypnotic setting (the so-called London-Fuhrer design). So it remains possible that hypnosis is not necessary. From the empirical literature, however, it is generally found that hypnosis boosts the effect of suggestion (though it’s disputed why; some of it is just that the Gandhi-Oakley finding that the word “hypnosis” increases suggestibility in and of itself). My best guess is that hypnosis adds considerably to the effect given that, if not, the effect of suggestion on working memory performance would have been discovered a long time ago in studies of psychotherapeutic treatment following acquired brain injury.